Designing a nanodevice including taking pictures of nanowires with 4 landmarks, importing pictures in Klayout (a free layout editor), aligning image landmarks to pre-patterned layout landmarks (see figures below), and drawing patterns such as source, drain, or gate for lithography.
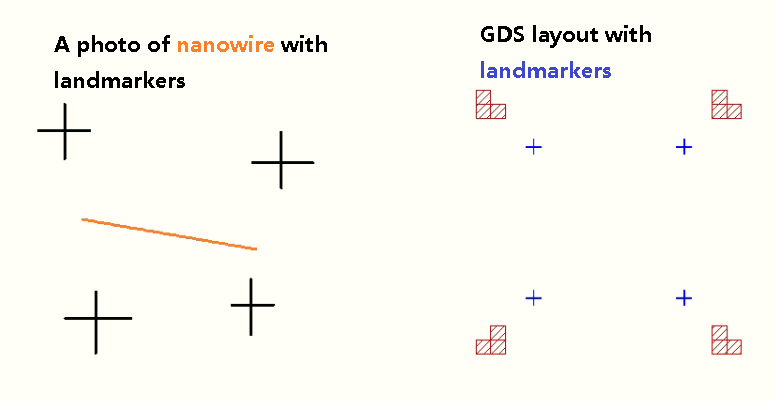
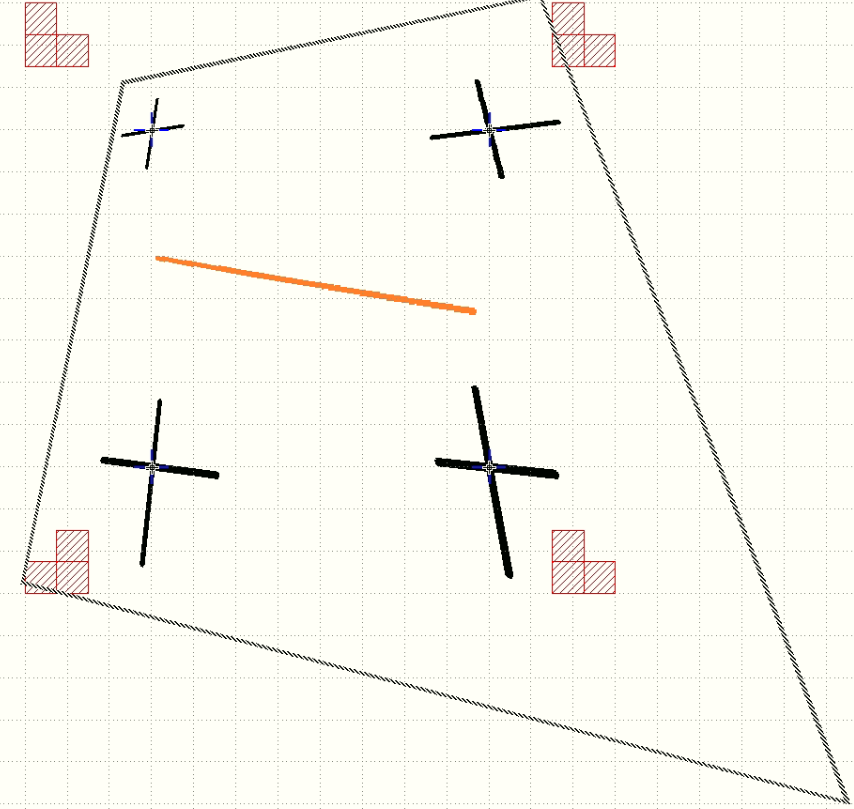
To automate the alignment, we need to calculate transform matrice. The formula is very complicated according to this post. However, I found a simpler one in Zhaoen’s PKout 2.0 for KLayout. The snippet is shown as follows (the script can be found here)
def _toTransMatrix(self,marks):# modified from Zhaoen's PKout
'''marker: [[x1,y1],[x2,y2],[x3,y3],[x4,y4]], calculate trans matrix for this marker'''
m = np.ones([4,3])# 3d mark positions [[x1,y1,1],[x2,y2,1],[x3,y3,1],[x4,y4,1]]
m[:,0:2] = marks
M = np.matrix(m[:3,:]).T#[[x1,x2,x3],[y1,y2,y3],[1,1,1]], now M*(1,0,0)=p1 (frist point),M*(0,1,0)=p2 ,M*(0,0,1)=p3
V_p4 = m[3]#[x4,y4,1]
V = M.I.dot(V_p4)#so that M*V = V_p4
A = M*np.matrix(np.diagflat(V))#now we have A*[1,1,1] = V_p4, and lines A*[100],[010],[001] intersect with plane [001] at p1,p2,p3, A is the transform Matrix for ldMarks
return A
def toMatrix(self,ldMarks,gdsMarks):# modified from Zhaoen's PKout
'''calculate trans matrix'''
A = self._toTransMatrix(ldMarks)
B = self._toTransMatrix(gdsMarks)
return np.array(B*(A.I))
The 2D coordinates are first converted to 3D, $[x_i, y_i] \rightarrow [x_i, y_i, 1]$, i = 1, 2, 3, 4. _toTransMatrix returns the transform matrix A from $[1,0,0],[0,1,0],[0,0,1],[1,1,1]$ to $[x_i,y_i,1]$ i = 1 ,2, 3, 4. toMatrix returns the transform marix from image landmarkers to layout (gds) landmakers, which is what we need.
The transformation $[x,y,z] \rightarrow T_M [x,y,z]$ is performed by carrying out the matrix multiplication $f_M([x,y,z]) = M \cdot [x,y,z]^T$ followed by the perspective divide P, $P([x,y,z]) = [x/z,y/z,1]$ if $z!=0$ else $[x,y,z]$. We have $T_M = P f_M$, $T_{M1}T_{M2} = P f_{M1} P f_{M2} = P f_{M1} f_{M2} = T_{M1 M2}$.