For a single dot:
\[H = \epsilon (n_\uparrow + n_\downarrow) + U n_\uparrow n_\downarrow + \Delta (c^\dagger_\uparrow c^\dagger_\downarrow + c_\downarrow c_\uparrow)\]Let $\left|n_\uparrow n_\downarrow\right> = \left|00\right>,\left|01\right>,\left|10\right>,\left|11\right>$ be the basis, we have
\[c_\uparrow = \begin{bmatrix} 0 & 0&1 &0\\ 0 &0& 0&1\\ 0&0 & 0&0\\ 0& 0&0 &0\\ \end{bmatrix}\] \[c_\downarrow = \begin{bmatrix} 0 & 1&0 &0\\ 0 &0& 0&0\\ 0&0 & 0&-1\\ 0& 0&0 &0\\ \end{bmatrix}\]So
\[H = \left[ \begin{array}{cccc} 0 & 0 & 0 & \Delta \\ 0 & \epsilon & 0 & 0 \\ 0 & 0 & \epsilon & 0 \\ \Delta & 0 & 0 & U+2 \epsilon \\ \end{array} \right]\]Eigensystem (by Mathematica):
\[\left( \begin{array}{cccc} \epsilon & \epsilon & -\sqrt{\Delta ^2+\frac{U^2}{4}+U \epsilon +\epsilon ^2}+\frac{U}{2}+\epsilon & \sqrt{\Delta ^2+\frac{U^2}{4}+U \epsilon +\epsilon ^2}+\frac{U}{2}+\epsilon \\ \{0,0,1,0\} & \{0,1,0,0\} & \left\{-\frac{\sqrt{\Delta ^2+\frac{U^2}{4}+U \epsilon +\epsilon ^2}+\frac{U}{2}+\epsilon }{\Delta },0,0,1\right\} & \left\{-\frac{-\sqrt{\Delta ^2+\frac{U^2}{4}+U \epsilon +\epsilon ^2}+\frac{U}{2}+\epsilon }{\Delta },0,0,1\right\} \\ \end{array} \right)\]The ground state energy can be either $\epsilon$ or $-\sqrt{\Delta ^2+\frac{U^2}{4} + U \epsilon + \epsilon ^2} + \frac{U}{2}+\epsilon$, the transition happens when these two energies are equal, that is
\[\frac{U^2}{4} = \Delta^2 + (\frac{U}{2}+\epsilon)^2\]or (can U be negative?)
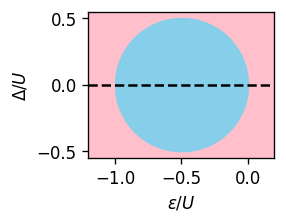
P.S.
If $U = 0$, the spectrum is ${E_1,E_2,E_3,E_4} = {\epsilon,\epsilon,-\sqrt{\Delta^2+\epsilon^2}+\epsilon,\sqrt{\Delta^2+\epsilon^2}+\epsilon}$. The ground state engergy is $E_3$. The excitation energy is $\sqrt{\Delta^2 + \epsilon^2}$ or $2\sqrt{\Delta^2 + \epsilon^2}$.
We then try the BdG Hamiltonian mentioned in this post as an exercise.
\[\begin{align} H &= \epsilon (n_\uparrow + n_\downarrow) + \Delta (c^\dagger_\uparrow c^\dagger_\downarrow + c_\downarrow c_\uparrow)\\ &= \epsilon (c_\uparrow^\dagger c_\uparrow + c_\downarrow^\dagger c_\downarrow) + \Delta(...)\\ &= \frac{\epsilon}{2}(c_\uparrow^\dagger c_\uparrow + c_\uparrow^\dagger c_\uparrow + c_\downarrow^\dagger c_\downarrow + c_\downarrow^\dagger c_\downarrow) + \Delta(...)\\ &=\frac{\epsilon}{2}(c_\uparrow^\dagger c_\uparrow + 1-c_\uparrow c_\uparrow^\dagger + c_\downarrow^\dagger c_\downarrow + 1-c_\downarrow c_\downarrow^\dagger) + \Delta(...)\\ &=\epsilon + \frac{\epsilon}{2}(c_\uparrow^\dagger c_\uparrow -c_\uparrow c_\uparrow^\dagger + c_\downarrow^\dagger c_\downarrow -c_\downarrow c_\downarrow^\dagger) + \Delta(c^\dagger_\uparrow c^\dagger_\downarrow + c_\downarrow c_\uparrow)\\ &=\epsilon + \frac{\epsilon}{2}(c_\uparrow^\dagger c_\uparrow -c_\uparrow c_\uparrow^\dagger + c_\downarrow^\dagger c_\downarrow -c_\downarrow c_\downarrow^\dagger) + \frac{\Delta}{2}(c^\dagger_\uparrow c^\dagger_\downarrow - c^\dagger_\downarrow c^\dagger_\uparrow + c_\downarrow c_\uparrow - c_\uparrow c_\downarrow) \end{align}\]Let $c_\uparrow,c_\downarrow,c_\uparrow^\dagger,c_\downarrow^\dagger$ be $(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)$, we have,
\[c_\uparrow^\dagger c_\uparrow = (1,0,0,0)^\dagger (1,0,0,0)\\ = \begin{bmatrix} 1 & 0&0 &0\\ 0 &0& 0&0\\ 0&0 & 0&0\\ 0& 0&0 &0\\ \end{bmatrix}\]Drop the constant $\epsilon$ in the first term of $H$, we have the BdG Hamiltonian
\[H_{BdG} = \frac{1}{2} \begin{bmatrix} \epsilon & & &\Delta\\ &\epsilon&-\Delta &\\ &-\Delta&-\epsilon&\\ \Delta& & &-\epsilon\\ \end{bmatrix}\]Find the eigensystem with Mathematica:
\[\left( \begin{array}{cccc} -\frac{1}{2} \sqrt{\Delta ^2+\epsilon ^2} & -\frac{1}{2} \sqrt{\Delta ^2+\epsilon ^2} & \frac{1}{2} \sqrt{\Delta ^2+\epsilon ^2} & \frac{1}{2} \sqrt{\Delta ^2+\epsilon ^2} \\ \left\{-\frac{\sqrt{\Delta ^2+\epsilon ^2}-\epsilon }{\Delta },0,0,1\right\} & \left\{0,-\frac{\epsilon -\sqrt{\Delta ^2+\epsilon ^2}}{\Delta },1,0\right\} & \left\{-\frac{-\sqrt{\Delta ^2+\epsilon ^2}-\epsilon }{\Delta },0,0,1\right\} & \left\{0,-\frac{\sqrt{\Delta ^2+\epsilon ^2}+\epsilon }{\Delta },1,0\right\} \\ \end{array} \right)\]That is $E = \pm \sqrt{\epsilon^2 + \Delta^2}/2$, the excitation energy is $\sqrt{\epsilon^2 + \Delta^2}$.
P.S. 2 GitHub pages have troubles when there is a “|” in an inline equation.